Loi d'Ohm pour une chaîne complète et pour une section de chaîne : options d'écriture de la formule, description et explication
Il n’existe aucun moyen pour un électricien professionnel ou un électronicien de contourner la loi d’Ohm dans ses propres activités, en résolvant les problèmes liés à l’installation, au réglage et à la réparation des circuits électroniques et électriques.
En fait, tout le monde doit comprendre cette loi. Parce que tout le monde est confronté à l’électricité au quotidien.
Et bien que la loi d’Ohm du physicien allemand soit prévue dans le programme du secondaire, dans la pratique, elle n’est pas toujours étudiée à temps. Par conséquent, dans notre matériel, nous examinerons un sujet aussi pertinent pour la vie et comprendrons les options d'écriture de la formule.
Le contenu de l'article :
Section unique et circuit électrique complet
Considérant un circuit électrique du point de vue de l'application de la loi d'Ohm à un circuit, il convient de noter deux options de calcul possibles : pour une section distincte et pour un circuit à part entière.
Calcul du courant d'une section de circuit électrique
En règle générale, une section d'un circuit électrique est considérée comme la partie du circuit qui exclut la source de CEM, car ayant une résistance interne supplémentaire.
Par conséquent, la formule de calcul, dans ce cas, semble simple :
Je = U/R,
Où respectivement :
- je – la force actuelle ;
- U – tension appliquée ;
- R. - résistance.
L'interprétation de la formule est simple : le courant circulant dans une certaine section du circuit est proportionnel à la tension qui lui est appliquée et la résistance est inversement proportionnelle.
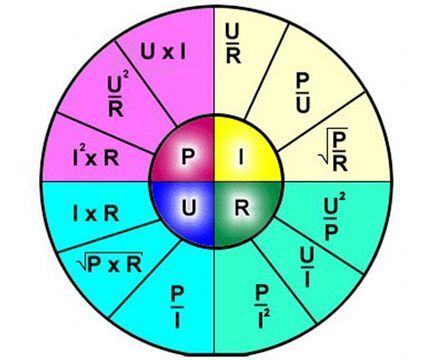
Ainsi, la formule décrit clairement la dépendance du flux de courant à travers une section distincte du circuit électrique par rapport à certaines valeurs de tension et de résistance.
La formule est pratique à utiliser, par exemple, lors du calcul des paramètres de la résistance qui doit être soudée dans le circuit si la tension et le courant sont donnés.
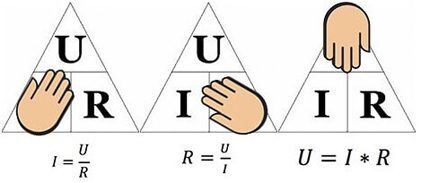
Le chiffre ci-dessus permettra de déterminer, par exemple, le courant circulant dans une résistance de 10 ohms à laquelle une tension de 12 volts est appliquée. En remplaçant les valeurs, nous trouvons – I = 12 / 10 = 1,2 ampères.
Les problèmes de recherche de résistance (lorsque le courant et la tension sont connus) ou de tension (lorsque la tension et le courant sont connus) sont résolus de la même manière.
Ainsi, vous pouvez toujours sélectionner la tension de fonctionnement requise, l'intensité du courant requise et l'élément résistif optimal.
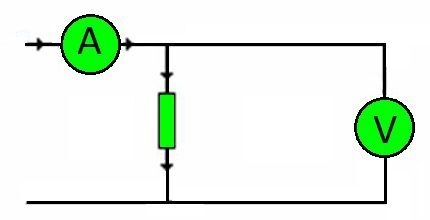
À propos, les fils de connexion de n’importe quel circuit sont des résistances. La quantité de charge qu’ils doivent supporter est déterminée par la tension.
En conséquence, toujours en utilisant la loi d’Ohm, il devient possible de sélectionner avec précision la section de conducteur requise, en fonction du matériau de l’âme.
Nous avons des instructions détaillées sur notre site Web calcul de la section du câble en termes de puissance et de courant.
Option de calcul pour une chaîne complète
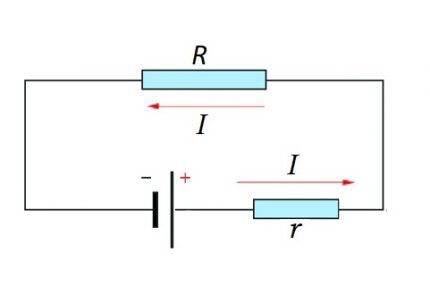
Un circuit complet est composé d'une ou plusieurs sections, ainsi que d'une source de CEM. Autrement dit, la résistance interne de la source EMF est ajoutée au composant résistif existant de la section du circuit.
Il est donc logique de modifier légèrement la formule ci-dessus :
je = U / (R + r)
Bien entendu, la valeur de la résistance interne de la FEM dans la loi d’Ohm pour un circuit électrique complet peut être considérée comme négligeable, bien que cette valeur de résistance dépende en grande partie de la structure de la source de FEM.
Cependant, lors du calcul de circuits électroniques complexes, de circuits électriques comportant de nombreux conducteurs, la présence d'une résistance supplémentaire est un facteur important.
Tant pour une section d'un circuit que pour un circuit complet, le moment naturel doit être pris en compte - l'utilisation d'un courant constant ou variable.
Si les points mentionnés ci-dessus, caractéristiques de la loi d’Ohm, étaient considérés du point de vue de l’utilisation du courant continu, tout semble quelque peu différent avec le courant alternatif.
Prise en compte de l'effet de la loi sur une quantité variable
La notion de « résistance » aux conditions de passage du courant alternatif doit être considérée davantage comme la notion d'« impédance ». Il s'agit de la combinaison d'une charge résistive (Ra) et d'une charge de résistance réactive (Rr).
De tels phénomènes sont provoqués par les paramètres des éléments inductifs et les lois de commutation par rapport à une valeur de tension variable - une valeur de courant sinusoïdal.
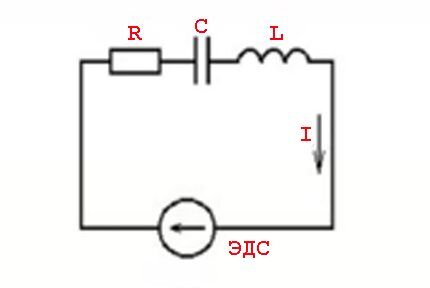
En d'autres termes, il existe un effet des valeurs de courant en avance (décalage) des valeurs de tension, qui s'accompagne de l'apparition de puissances actives (résistives) et réactives (inductives ou capacitives).
De tels phénomènes sont calculés à l'aide de la formule :
Z = U/I ou Z = R + J * (XL -XC)
Où: Z – l'impédance ; R. – charge active ; XL , XC – charge inductive et capacitive ; J. -coefficient.
Connexion série et parallèle des éléments
Pour les éléments d'un circuit électrique (section d'un circuit), un point caractéristique est une connexion série ou parallèle.
En conséquence, chaque type de connexion s’accompagne d’un modèle différent de flux de courant et d’alimentation en tension.À cet égard, la loi d'Ohm s'applique également différemment, selon la possibilité d'inclure des éléments.
Circuit d'éléments résistifs connectés en série
Par rapport à une connexion en série (une section d'un circuit à deux composants), la formulation suivante est utilisée :
- je = je1 =Je2 ;
- U = U1 +U2 ;
- R = R1 +R2
Cette formulation démontre clairement que, quel que soit le nombre de composants résistifs connectés en série, le courant circulant dans une section du circuit ne change pas de valeur.
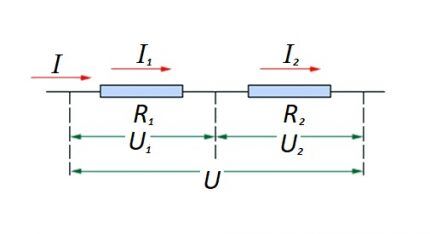
L'amplitude de la tension appliquée aux composants résistifs efficaces du circuit est la somme et totalise la valeur de la source emf.
Dans ce cas, la tension sur chaque composant individuel est égale à : Ux = I * Rx.
La résistance totale doit être considérée comme la somme des valeurs de tous les composants résistifs du circuit.
Circuit d'éléments résistifs connectés en parallèle
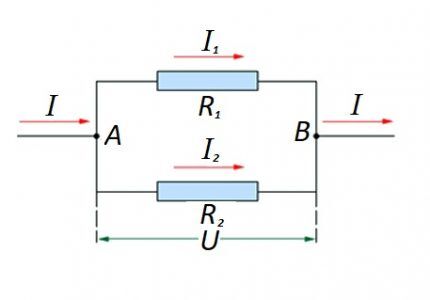
Dans le cas d'une connexion parallèle de composants résistifs, la formulation suivante est considérée comme juste par rapport à la loi du physicien allemand Ohm :
- je = je1 +Je2 … ;
- U = U1 =U2 … ;
- 1/R = 1/R1 + 1/R2 + …
Les options permettant de créer des sections de circuit de type « mixte », lorsque des connexions parallèles et série sont utilisées, ne sont pas exclues.
Pour de telles options, le calcul est généralement effectué en calculant initialement la résistance résistive de la connexion parallèle. Ensuite, la valeur de la résistance connectée en série est ajoutée au résultat obtenu.
Formes intégrales et différentielles du droit
Tous les points ci-dessus avec calculs sont applicables aux conditions dans lesquelles des conducteurs de structure pour ainsi dire «homogène» sont utilisés dans des circuits électriques.
Pendant ce temps, dans la pratique, il faut souvent s'occuper de la construction de schémas, où la structure des conducteurs change selon différentes sections. Par exemple, des fils de section plus grande ou, au contraire, plus petite, fabriqués à partir de matériaux différents, sont utilisés.
Pour tenir compte de ces différences, il existe une variante de la « loi d’Ohm différentielle-intégrale ». Pour un conducteur infinitésimal, le niveau de densité de courant est calculé en fonction de la valeur de tension et de conductivité.
La formule suivante est utilisée pour le calcul différentiel : J = ό * E
Pour le calcul intégral, la formulation est donc : je * R = φ1 – φ2 + έ
Cependant, ces exemples sont plutôt plus proches de l’école de mathématiques supérieures et ne sont pas réellement utilisés dans la pratique réelle d’un simple électricien.
Conclusions et vidéo utile sur le sujet
Une analyse détaillée de la loi d'Ohm dans la vidéo ci-dessous permettra enfin de consolider les connaissances dans ce sens.
Une leçon vidéo unique renforce qualitativement la présentation écrite théorique :
Le travail d’un électricien ou l’activité d’un électronicien est intégralement lié aux moments où il faut effectivement observer la loi de Georg Ohm en action. Ce sont des truismes que tout professionnel devrait connaître.
Des connaissances approfondies sur cette question ne sont pas requises - il suffit d'apprendre les trois principales variantes de la formulation pour l'appliquer avec succès dans la pratique.
Souhaitez-vous compléter le matériel ci-dessus avec des commentaires précieux ou exprimer votre opinion ? Veuillez écrire des commentaires dans le bloc sous l'article. Si vous avez des questions, n'hésitez pas à les poser à nos experts.



